*** DRAFT ***
Variance Reduction Techniques applied to large
scale simulation models
Steven R. Gould
Formerly with
Royal Aerospace Establishment
Farnborough
[Although the work was carried out at RAE, Farnborough this
was back in the summer of 1989. The author can now be contacted
via e-mail. Note that
this is only a draft - any comments would be more than welcome.
Thanks!]
Table of Contents:
Keywords: simulation, variance
reduction techniques (VRT), modelling
ABSTRACT
Large scale simulation models are often very complex and
require long run-times. As a result, it is often desirable to
make them more precise so that a greater degree of accuracy may
be achieved without increasing these times. One way in which this
may be done is by the use of Variance Reduction Techniques. This
paper discusses the application of a number of these techniques
to large scale models at the Royal Aerospace Establishment (RAE),
Farnborough. Where variance reductions were poor, it suggests why
this may be so and gives possible ways of improving these. A
modification to the antithetic variates variance reduction
technique is proposed to make it more suitable to large, complex
models. Of particular interest is the successful application of
martingales and control variates to two of the models.
INTRODUCTION
Many simulation studies aim to estimate the steady-state mean
of some performance parameter. The usual method of increasing the
accuracy of such estimates is simply to increase the number N
of replications of the model. However, the precision of such
stochastic simulation estimators only increases as the square
root of the computational effort; ie. 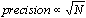 . .
In the situations studied in this paper, it is not desirable
to continue increasing N indefinitely until the required
accuracy is reached simply because the time required would be
unacceptable. It is therefore necessary to look at ways of
increasing the accuracy of the estimators without increasing the
number of replications N. Such methods of manipulating the
simulation so as to improve the accuracy of the estimators are
known as Variance Reduction Techniques (VRTs).
BACKGROUND
Part of the RAEs work involves studying the effectiveness of
various methods of air-to-ground attacks on mobile targets. A
major part of this process makes use of a number of large scale
simulation models. The major one studied in this paper simulates
the end-game effectiveness of different weapon systems upon
different target arrangements.
The model studied is of a replicative nature
-- that is one run (or replication) of the model simulates one
possible outcome from start to finish. To
obtain a reasonable estimate of the parameter of interest, it is
therefore necessary to perform a (possibly large) number of such
replications and take, say, the mean of these observations. This
is in contrast to a regenerative simulation
model where some number, n, of runs/trials are made by
dividing one long run into n independent runs post hoc.
INITIAL RESULTS ON A MORE
COMPLEX MODEL
An earlier study[1] by the author on a similar, but more
complex model provided valuable experience and results on which
to base this work. The main points resulting from this earlier
work are summarised below:
Antithetic Variates[2]
These gave some promising variance reductions for small test
runs with n = 2 x 20 antithetic pairs. However, as n
was increased the variance reductions seemed to disappear and
some large variance productions were observed. The
reason for such disappointing results was found to be that the
antithetic pairs were not strongly negatively correlated as
required. Due to the great complexity of the model, the long
chain of random events seemed to remove any negative correlation
"created", leaving antithetic runs with an almost
random correlation.
For this reason the antithetic variates VRT is not really
suited to large, complex models. However better results may be
possible in such models if it is possible to apply modified
antithetic variates as described below.
Modified Antithetic Variates
We are interested in outcomes resulting from the latter stages
of the implementation. It may therefore be more appropriate to
use random numbers a0, a1,
..., ak-1 for the earlier stages of the
simulation, for both antithetic runs; then, only after a series
of interesting events occur, switch over to using ak,
ak+1, ..., aK and (1 -
ak), (1 - ak+1),
..., (1 - aK) as the random numbers for the
antithetic pairs. For example, if we wait until the aircraft has
released it weapon(s) before applying antithetic random numbers,
then the result may be more precise.
This may seem a strange idea to grasp at first, because we
are, in effect, ensuring a positive correlation. However this
only continues up to some predetermined point, after which the
usual antithetic variates VRT is applied. By doing this we ensure
that two similar circumstances have antithetic variates applied
to them, hence the corresponding outcomes should be more
negatively correlated.
Consider the case where we wait until a weapon is released
before applying antithetic variates. We are really concerned with
a sub-model of the simulation; one which models the actual weapon
attack. Since other "external" factors need to be
considered when evaluating any system, it is necessary to
simulate any important events up to this point. We then enter the
sub-model with a random set of inputs which is the same for both
antithetic runs. Performance within the sub-model is then
subjected to the antithetic variates VRT, where the outcomes are
more strongly (negatively) correlated than before. The result
will be a more precise estimate of the performance parameters of
interest. This process may be illustrated as :

Figure 1.
Justification of this idea lies in the fact that antithetic
variates can produce quite significant variance reductions when
applied to one random event. Good variance reductions may also be
possible with two or three random events happening in series, as
is the case in many academic examples. However, as the chain of
random events is extended, the negative correlation between
outcomes is reduced until the point where, after a long sequence
of such events, there is virtually zero correlation between the
runs. This will be the case particularly in large complex models
such as those studied here, and is illustrated by the poor
results obtained.
By cutting down the sequence of events to consider only those
of greatest interest, it is possible to maintain a good negative
correlation between runs. Hence, we have justified the
consideration of some small sub-model, to which the antithetic
variates VRT is applied, as a means of improving the
effectiveness of the technique.
Correlated Sampling[3,4]
This gave the best variance reductions of all VRTs applied to
this model and, in fact, was one of the easiest to implement. The
worst variance reduction was a reasonable +14.2%, however this
was with only 2 sets of 40 observations. For larger numbers of
observations (say >= 100), the worst variance reduction
was a good +23.7%. These worst cases contrasted with variance
reductions of up to 88%. Typically, though, variance reductions
of about 50-55% were usual.
Control Variates[5]
Control variables were constructed reflecting the level of
attrition on the aircraft carrying the weapon systems. Provided
the number of replications (n) was large compared to the
number of control variables (m=10), then variance
reductions were observed for all estimators. Significant bias
seemed to be associated with the larger variance reductions (of
up to 51.6%) achieved, perhaps as a result of performing too few
replications. However using Jackknifed regression[6] to provide
more robust estimates had only a very small affect on the already
large variance reductions. In contrast, where there had been only
small variance reductions (of between 1.5% and 9.0%), the bias in
the estimators was insignificant - the control variables used
were not so relevant to these performance parameters.
Overall, stable variance reductions were achieved provided n
>> m, however the magnitude of these improvements was
slightly disappointing. The reason for only small variance
reductions was due mainly to the choice of control variables and
also due to a "quirk" in the model. If good
control variables were found then we could of expected greater
variance reductions.
Martingales[7]
Martingales reflecting detection/hit/kill probabilities were
used and gave some poor results. The main reason for this was
thought to be that they try to reduce random variation in the
results, whereas this only makes up a small part of the overall
variation - the main source being from the distribution and
density of targets relative to submunition release points. The
martingales used did not even attempt to reduce this. A later
observation suggested that a relatively small number of
replications relative to the number of martingales may also have
contributed to the poor results.
If the main source of variation can however be identified,
more suitable martingales may be constructed. In such cases, it
was felt that martingales, like the control variables on which
they are based, could offer potentially large variance
reductions.
FURTHER ANALYSIS
Based upon these initial results, it was decided to look at
another similar model which simulated attacks of different weapon
systems from target acquisition through to weapon impact. This
model was often used for large numbers of runs with many
different scenarios and, as a result, an improvement in accuracy
was desirable.
Modified antithetic variates
The first stage in the implementation of modified antithetic
variates involved applying the full antithetic variates VRT. This
meant changing the model so that every process within it used a
different random number stream.
Once the full antithetic variates VRT had been implemented, it
was necessary to identify where the main source of variance
arose. From previous work on the more complex model, it had been
found that the main variance was not due to
randomness in the detection, hit or kill of individual targets,
but occurred at some stage before this. As a result it was
decided to try implementing modified antithetic variates from the
dispense of submunitions onwards. This gave small improvements
over normal antithetic variates, however the results were still
disappointing with small variance reductions and even, in some
cases, variance productions.
Other points in the model were tried, for example, dispenser
flyout. However similarly poor results were observed. The reason
behind this was that the major source of variation had not been
identified and, as a result, good negative correlations
between the runs were not being achieved. Consequently, it was
decided that the model was too complex for antithetic variates
(and even modified antithetic variates) to be of any significant
use, and that time spent persueing it would be better spent
looking at other techniques.
Martingales and Control Variates
Table 1 (below) shows the
development in the selection of martingales and control variates
for the model of weapon system 1. When a variable likely to be a
good control variable / martingale was found it was tested on the
base case along with the current "best" set of
variables. If any variance production was detected in
targets hit/killed then this variable was labelled as unsuitable
and dropped from further tests.
Table 1. Development in
the selection of Martingales and Control Variables
PARAMETER 1 PARAMETER 2 PARAMETER 3
std. jack- std. jack- std. jack-
knifed knifed knifed
Dispenser/submunition 1 M 2.1 2.1 4.7 5.0 +0.3 +0.2
reliability
Detection/Hits/Kills 6 M 2.4 2.5 22.4 22.8 +0.0 -0.1
martingales
Aircraft positioning 1 CV 32.4 35.0 46.5 48.8 -0.5 -0.2
Pilot steering error 1 CV (2.2) (2.0) (22.3) (22.4) (-0.2) (-0.6)
Dispenser errors 4 CV (32.0) (34.1) (46.1) (48.0) (-0.2) (-1.2)
Target separation 2 CV (32.1) (34.5) (46.3) (48.5) (-1.0) (-1.2)
Notes:
- Figures in brackets indicate variance production over the
previous "best" set of control variables;
consequently the new control variable(s) were dropped
from further tests.
- All results here are for the base case only, however
relative variance reductions would be similar for other
cases.
- M indicates martingale; CV indicates control variable in
column 2 of the table.
Note that it would have been easy to find several more
possible martingales and control variables, however these would
only have been relevant to certain scenarios. The set described
below however was generally applicable to all
runs of the weapon system 1 model.
Dispenser / Submunition reliability martingale
This martingale reflects the reliability of the dispensers and
submunitions in weapon system 1. In any one replication, it sums
all attempts to release dispensers and submunitions, in the one
martingale.
Let the dispensers have a reliability (ie. probability of
working) of reld and submunitions a
reliability of rels. Assume there are ns
submunitions per dispenser, then we can construct a martingale in
the following way.
At the beginning of each replication the martingale is
initialised to zero. It is then updated whenever an attempt is
made to dispense a submunition or in the event of dispenser
failure.
The binary variable used to construct the martingale is that
of a successful / unsuccessful submunition dispense. If a
submunition is dispensed as intended the martingale would be
incremented by 1 - (reld.rels)
(occurring with a probability of reld.rels).
However, if a submunition failed to work (this would happen with
a probability reld.(1 - rels)
), the martingale would be incremented by 0 - reld.rels
representing the failure.
The only other case to consider now is that of dispenser
failure -- this occurs with probability (1 - reld)
and may be regarded as the combined failure of ns
submunitions. Hence the martingale increment in this case is ns.(0
- reld.rels).
It is easy to show that the expected value of this martingale
is zero simply by considering the martingale increment for each
event, multiplying by the expected number of submunitions
affected and summing over all events.
Detection/Hit/Kill martingales
For completeness, detection/hit/kill martingales were
constructed for all target types using binary variables
indicating the success or failure of each event. However due to
the nature of the input data / program some of these were of no
use. For example, where the probability of some event occurring
is p=1.0 the martingale increment will always be 1-p=0.0,
hence its sum will always be zero.
The remaining martingales reflected the "luck" in
detection/hits/kills of certain targets. These were found to
produce variance reductions (see table 1)
in parameter 1 and especially in parameter 2.
Aircraft position (Control Variable)
A Normal[0,1] variable is selected by the program to give
random variation on the aircrafts position relative to the target
array. By using this as a control variable along with the above
martingales, variance reductions of up to 50% in parameter 2, and
35% in parameter 1, were observed. Since this variable was common
to all weapon systems within the model, it could
have been applied, without any modification, to other systems and
expected to give similar variance reductions.
The other control variables listed in table
1 were found to cause small variance productions for
the base case and, as a result, were not adopted. [Note that
tables 1, 2
and 3 give variance reductions
achieved using both standard regression and the
more robust jackknifed regression.]
Using this set of martingales and control variables, a number
of tests were performed simply by varying some of the input
parameters of the model. A summary of the variance reductions
obtained in these tests is given in table
2.
By using standard regression to estimate the control variable
coefficients, variance reductions on parameter 1 ranged from a
small 1.0% up to a very good 56.7%, with an average of around
25%. Ashford and Beales cross-estimation test[6] revealed that
the bias in the estimates of parameter 1 was very small and that
it was not significant. Although, on average, the more robust
jackknifed regression provided marginally greater variance
reductions there is no reason to believe that this will always be
the case. In fact, in just over half of the tests it was found to
produce slightly worse variance reductions.
The variance reductions achieved for parameter 2 were
considerably higher than for parameter 1. Although typically
around 50%, variance reductions were observed from a very
reasonable 25.9% up to an excellent 75.6% using standard
regression. Again, bias was very small and not significant, and
jackknifed regression provided similar reductions in variance.
The main reason for the large variance reductions in parameter 2
compared to parameter 1 was that one of the martingales used was
strongly-correlated with it -- refer back to table 1.
Although parameter 3 was one of the main parameters of
interest, the variance of its estimate was smaller than that of
parameters 1 and 2. Consequently it was already estimated to a
sufficiently high degree of accuracy, and therefore was not of
great importance when looking for control variables. None of the
martingales or control variables looked at were particularly
well-correlated with this parameter -- hence the variance
reductions observed on it were small (see table 2).
Table 2. Control Variates
Variance Reductions
A few examples with the model of weapon system
1*
PARAMETER 1 PARAMETER 2 PARAMETER 3
Input parameters varied std. jack- std. jack- std. jack- n
knifed knifed knifed
Base Case 67.5 67.8 72.0 72.4 +1.1 +0.3 999
Random number seed 66.9 66.9 70.5 70.6 +1.1 +0.4 558
Attack angle 72.6 72.1 81.1 80.7 +0.5 +0.2 590
Attack angle 71.5 71.2 75.0 74.6 +0.3 +1.0 593
Kill probability 65.6 65.6 70.3 70.3 +2.0 +0.8 534
Target speed, attack angle 73.4 73.1 83.2 82.9 +1.5 +0.6 548
Target speed, attack angle 85.5 85.3 85.9 85.6 +1.8 +1.1 573
Target separation 67.1 68.4 70.5 71.9 -2.7 -0.1 564
Target separation 78.6 77.6 82.8 81.8 +0.8 -1.1 560
Ranging errors 29.0 26.7 74.2 73.5 +0.9 +0.1 572
Terrain 67.0 66.6 72.4 72.3 +1.5 +0.6 787
Attack angle 42.8 42.9 54.8 54.7 -0.4 -1.1 579
Target array 1 69.5 69.2 70.7 70.6 +1.4 -0.1 592
Target array 2 54.1 54.8 58.9 59.8 -1.8 -1.7 566
Target array 3 49.8 48.7 59.5 59.5 -0.2 +1.6 569
Target array 4 53.1 52.8 61.3 61.2 +0.2 -0.2 567
Target array 5 66.9 67.3 71.1 71.2 +5.8 +4.2 581
Ranging errors, terrain,
attack angle 8.9 7.7 60.6 60.2 +1.7 +1.0 765
Ranging errors, terrain,
attack angle 5.9 3.0 62.7 61.8 -0.4 +0.2 245
Mean variance reductions
(19 runs) 57.7 57.2 70.4 70.3 +0.8 +0.4
* The control variables used for these tests
consisted of: 1 dispenser/submunition martingale, 6
detection/hit/kill martingales, and 2 control variables for the
aircraft's position.
By looking at the coefficients generated from the regression
analysis it is possible to gain a greater insight as to what
influences the models outcomes. It is also useful in that any
peculiarities or irregularities in the model may be highlighted
by strange coefficients. For example, suppose the
dispenser/submunition reliability martingale was given a negative
coefficient. This would suggest that the greater the
number of submunitions successfully released, the lower
the expected number of target hits! Clearly this is not what we
would expect. By examining the coefficient obtained from the
regression we should see this, in which case it would be
necessary to seek some explanation of why this negative
correlation has arisen.
APPLICATION TO OTHER WEAPON SYSTEMS
All martingales and control variables described in the
previous section were chosen because they were relevant to any
scenario of the model of weapon system 1 and were generally
applicable to any other weapon system. For example, every weapon
system will have associated detect/hit/kill probabilities, and
also some form of dispenser / submunition combination with
associated reliabilities. As mentioned above, the aircraft
position control variable was common to all weapon systems.
Using this general set of martingales / control
variables as a starting point, we could expect to achieve similar
variance reductions for other weapon system models. It would then
be possible, perhaps even desirable, to look at individual weapon
system models and identify any weapon-system-dependent
martingales or control variables. Further variance reductions
would then be possible.
As an example it was decided to look at another weapon system
model (referred to here as weapon system 2). The general set of
martingales and control variables discussed previously was
implemented and variance reductions only slightly less (on
average) were observed. After looking at the model in more
detail, a further two martingales were constructed from
acceptance probabilities. These were similar to the detection
martingales but involved the acceptance of targets once detected.
The variance reductions achieved with the addition of these
two new martingales were now almost the same as those achieved
for weapon system 1 -- compare tables 2
and 3. The most significant
difference however was that variance reductions in excess of 50%
were observed for parameter 3 where previously there had been
almost none. This was due to the fact that just one of the two
extra martingales was very relevant to this parameter whereas
others used were only vaguely related.
Table 3. Control Variates
Variance Reductions
A few examples with the model of weapon system
2*
PARAMETER 1 PARAMETER 2 PARAMETER 3
Input parameters varied std. jack- std. jack- std. jack- n
knifed knifed knifed
Base Case 15.6 18.1 39.1 41.0 46.8 47.5 609
Random number seed 23.7 25.8 40.6 42.5 46.2 46.1 630
Attack angle 50.3 51.3 64.9 64.1 38.8 38.3 620
Attack angle 18.5 16.9 45.7 44.3 50.6 49.7 599
Kill probability 18.8 21.4 36.8 37.7 51.8 51.5 588
Target speed, attack angle 53.7 54.1 69.2 69.4 40.5 41.0 620
Target speed, attack angle 8.8 9.2 38.2 38.2 50.8 50.3 606
Target separation 30.8 31.5 44.3 44.7 50.5 49.3 592
Target separation 40.3 42.7 52.9 54.3 50.4 50.5 615
Ranging errors 18.8 18.1 53.2 52.8 48.1 47.2 608
Terrain 33.2 32.9 46.9 46.4 50.7 50.3 786
Attack angle 15.6 18.1 39.1 41.0 46.8 47.5 609
Target array 1 27.3 28.3 45.4 46.1 40.6 38.0 597
Target array 2 11.0 8.7 30.3 28.1 44.7 45.1 612
Target array 3 4.6 5.6 35.7 36.4 47.2 47.1 648
Target array 4 16.4 16.4 34.9 35.2 47.0 47.2 602
Target array 5 24.5 28.3 44.3 47.6 27.9 27.0 606
Ranging errors, terrain,
attack angle 14.1 15.2 46.1 47.5 48.2 48.8 814
Ranging errors, terrain,
attack angle 13.7 13.0 45.9 45.9 45.4 46.2 306
Mean variance reductions
(19 runs) 23.1 24.0 44.9 45.4 45.9 45.7
* The control variables used for these tests
consisted of: 1 dispenser/submunition martingale, 8
detect/accept/hit/kill martingales, and 1 control variable for
the aircraft's position.
CONCLUSIONS
The antithetic variates Variance Reduction Technique is not
really suited to large, complex simulation models such as those
studied here. A simple modification to the technique is proposed
to enable it to produce good variance reductions on more complex
models. This does, however, depend on the main source of
variation being in the latter stages of the simulation and
whether this can be successful identified. The modified
antithetic variates technique was applied to a large scale model,
but gave similarly poor results to the full technique. The main
reason behind its failure was that the main source of variation
had not been identified at this stage.
A set of martingales and control variables -- generally
applicable to all weapon system models -- were identified. They
were found to give good variance reductions on the two models to
which they were applied -- reductions in variance of up to 85%
were observed for one parameter.
Two model-dependent martingales were constructed for the
weapon system 2 model and gave further variance reductions.
The successful application of martingales and control
variates, and indeed many other VRTs not considered here, relies
upon a good understanding of the model. In this application,
previous work on a similar, but more complex model proved to be
very constructive, even though the variance reductions observed
then were by no means as significant. This goes to show that for
some types of simulation it is potentially very difficult to
achieve good variance reductions.
Finally, the application of martingales and control variates
to the large scale simulation models studied here was a great
success. The author strongly recommends the application of these
techniques to large scale simulation models when a reduction in
variance is required.
Acknowledgement -- I should like to thank Dr.
Robert Ashford of the University of Warwick for his helpful
comments and suggestions both in this work and in writing this
paper.
REFERENCES
[1] GOULD, S.R. (1989), The Effectiveness of Variance
Reduction Techniques Applied to the Simulation of Air-to-Ground
Line-of-Sight Engagements, Unpublished MOD(PE) Report
[2] HAMMERSLEY, J.M. and MORTON, K.W. (1956), A new Monte
Carlo technique : antithetic variates, Proc. Camb. Phil. Soc. 52,
449-475
[3] KAHN, H. (1950), Random Sampling (Monte Carlo) Techniques
in Neutron Attentuation Problems, Nucleonics 6(5),
6(6)
[4] KAHN, H. and MARSHALL A.W. (1953), Methods of Reducing
Sample Size in Monte Carlo Computations, Opns. Res. 1(5),
263-278
[5] LAVENBERG, S.S. and WELCH, P.D. (1981), A Perspective on
the Use of Control Variables to Increase the Efficiency of Monte
Carlo Simulations, Mgmt. Sci. 27, 322-335
[6] ASHFORD, R.W. and BEALE, E.M.L. (1989), A Cross-Estimation
Technique for using Control Variables in Stochastic Simulation, Eur.
J. Opl. Res. 40, 352-362
[7] ASHFORD, R.W. and BEALE, E.M.L. (1989), Using Martingales
to make Stochastic Simulations More Precise, Eur. J. Opl. Res.
38, 86-93
Feedback
So, what did you think? This is just a draft of this paper and
I would appreciate any comments or feedback you may have. Please
send comments via e-mail to the author.
|